Title: Statistical Mechanics at Strong Coupling: A Bridge between Landsberg’s Energy Levels and Hill’s Nanothermodynamics
Authors: Rodrigo de Miguel 1,* and J. Miguel Rubí2
1 Department of Teacher Education, Norwegian University of Science and Technology, 7491 Trondheim, Norway
2 Department of Condensed Matter Physics, University of Barcelona, 08007 Barcelona, Spain
*Author to whom correspondence should be addressed. Published in: Nanomaterials 2020, 10(12), 2471; https://doi.org/10.3390/nano10122471 (registering DOI)Received: 21 November 2020 / Revised: 3 December 2020 / Accepted: 6 December 2020 / Published: 10 December 2020 Abstract: We review and show the connection between three different theories proposed for the thermodynamic treatment of systems not obeying the additivity ansatz of classical thermodynamics. In the 1950s, Landsberg proposed that when a system comes into contact with a heat bath, its energy levels are redistributed. Based on this idea, he produced an extended thermostatistical framework that accounts for unknown interactions with the environment. A decade later, Hill devised his celebrated nanothermodynamics, where he introduced the concept of subdivision potential, a new thermodynamic variable that accounts for the vanishing additivity of increasingly smaller systems. More recently, a thermostatistical framework at strong coupling has been formulated to account for the presence of the environment through a Hamiltonian of mean force. We show that this modified Hamiltonian yields a temperature-dependent energy landscape as earlier suggested by Landsberg, and it provides a thermostatistical foundation for the subdivision potential, which is the cornerstone of Hill’s nanothermodynamics.
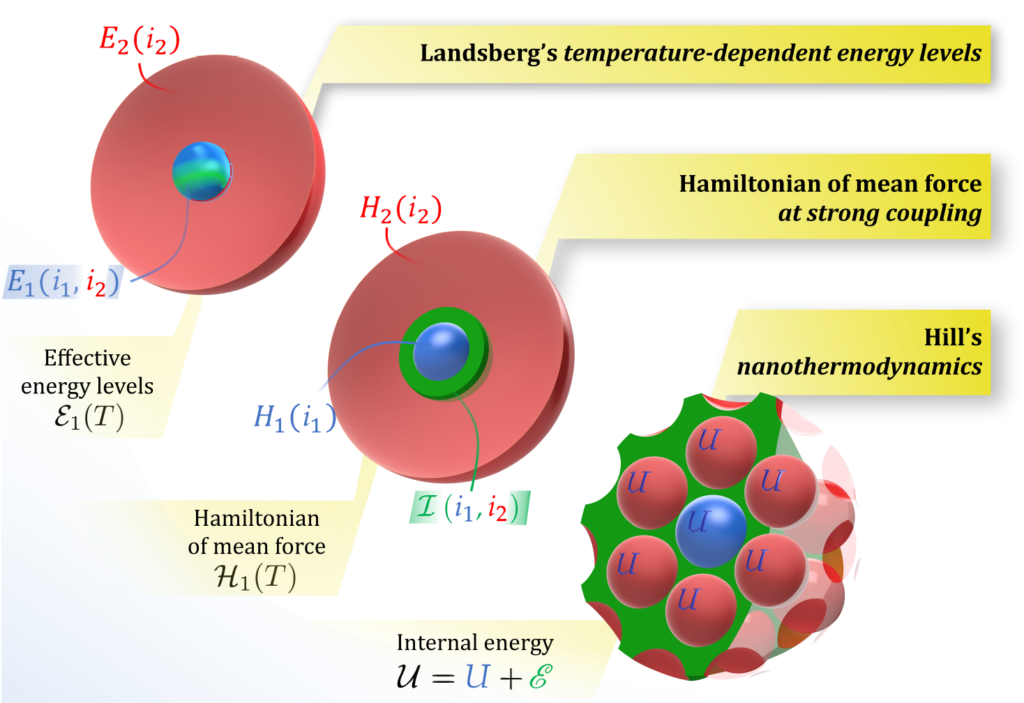
Figure 1. Illustration of the main features of the three small-system theories. In Landsberg’s theory, the energy levels ε1 of the system (blue sphere) are modified into ε1 due to its interaction with the (red) environment. Statistical mechanics at strong coupling starts with a total Hamiltonian consisting of the environment (red), the system (blue) and the interaction (green); averaging the system and the interaction over the environment results in a temperature-dependent Hamiltonian of mean force H1. Hill’s nanothermodynamics considers the system of interest as if it were surrounded by a macroscopic set of interacting replicas; the interaction causes the effective energy to depart from U and become U.
